4-1.一個物理問題中可能牽涉到許多個物理參數,而且參數之間彼此相關聯,造成分析時可能會十分複雜。因次分析便是依據相關的物理參數的因次,找出其中重要的無因次參數,以簡化問題之分析。
舉例而言,一個光滑的圓球在流體中運動,圓球所受之流體阻力FD與圓球直徑D,移動速度U,流體的密度ρ,動力黏滯係數μ有關。
利用這些參數的因次可以找出其間的關係。
4-2.白金漢(Buckingham) π 定律
「一個物理現象中有 n 個會影響到該現象的物理參數,在這些參數中若共有 m 個基本因次,則可找出 n - m 個獨立的無因次參數。」
基本因次:力 F(質量M)、時間 T、長度 L
舉例而言,一個光滑的圓球在流體中運動,圓球所受之流體阻力與圓球直徑D,移動速度U,流體的密度ρ,動力黏滯係數μ有關。
此問題中有 5 個物理參數,而參數中有 3 個基本因次,故應可找出 2 個無因次參數。
4-3.因次分析的方法:
A.逐步消去法(Step-by-step method):
逐步地消去所有影響參數中的力(質量)、時間及長度的因次:
(1)以函數的形式將所有的影響參數列出。
(2)將所有影響參數的因次以基本單位表示。
(3)以流體密度消去所有的參數中力或質量的因次。
(4)以流速消去所有的參數中時間的因次。
(5)以一個長度參數消去所有的參數中長度的因次。
(6)檢查所有的被消去因次的參數是否為無因次參數。
【例】
流體流經過一光滑的圓球,圓球所受之阻力FD與圓球直徑D,流速U,流體的密度ρ,動力黏滯係數μ有關。試找出其中的無因次參數
《解》
單位系統採用 MLT 系統
(1)以函數的形式列出所有的影響參數及其因次:
(2)以流體密度消去所有參數中力或質量的因次:
(3)以流速消去所有參數中時間的因次:
(4)以一個長度參數消去所有參數中長度的因次:
長度參數會選擇一個與流場有密切關係的特性長度,在此問題中圓球直徑D為具有代表性的長度參數
函數中的常數不需要一一列出
此問題中的無因次參數便是阻力係數CD和雷諾數 Re,且圓球之阻力係數為雷諾數 Re 的函數。
B.指數法(Exponent method):
可將影響參數以指數方程式的形式表示,再利用因次的一致性找出各參數的指數之間的關係。
(1)若影響參數超過5個時,可將參數分成 n - m - 1 組,每組有5 個參數。
(2)各組的影響參數必須包括有流體密度、速度及一個長度參數。
(3)將各組的影響參數以指數方程式的形式表示。
(4)利用基本因次(質量、時間、長度)的次方找出指數之間的關係。
(5)檢查具有相同指數的變數是否為無因次參數。
【例】
流體流經過一粗糙的圓球,直徑D,粗糙長度為ε的圓球,流速U,流體的密度ρ,動力黏滯係數μ。求與阻力FD有關的無因次參數。
《解》
此問題中共有6個物理參數,基本因次有3個,因此應該有3個無因次參數。採用指數法,必須將所有的影響參數分成 2 組:
第1組:
第2組:
第1組之指數方程式:
因基本因次的次方必須一致,故:
M 之因次:1 = c + d
L 之因次:1 = a + b - 3c - d
T 之因次:-2 = - a - d
將以上的聯立方程式求解可得:
c = 1 – d ; a = 2 – d ; b = 2 – d
指數方程式:
或
亦即
此問題中的無因次參數便是阻力係數 CD 和雷諾數 Re,且阻力係數為雷諾數 Re 的函數。
第2組之指數方程式:
基本因次的次方必須一致,故:
M 之因次:1 = c
L 之因次:1 = a + b - 3c + d
T 之因次: -2 = -a
求解可得: c = 1 ; a = 2 ; b = 2 – d
綜合第1組和第2組的結果:粗糙圓球的阻力係數為雷諾數 Re 及 相對粗糙度 ε/D 之函數:
值得注意:
(1) 無論逐步法或指數法皆可找出問題中重要的參數,且結果應相同。
(2) 但無因次參數可能會有不同的表示方式,譬如此問題亦可以表示為:
★因次分析可以找出問題中重要的無因次參數,但參數之間確切的函數關係還是無法由因次分析中得到,往往必須由實驗或理論解析求得其函數關係。
★
因次分析除簡化問題之分析外,用於實驗數據的整理,可使得實驗結果的表現方式更為簡明;譬如一個量測光滑圓球所受阻力的實驗,實驗中以三種不同直徑的圓球來進行實驗。依據因次分析找出此問題中重要的無因次參數:阻力係數CD及雷諾數Re。將阻力係數對雷諾數繪圖,會發現不同直徑球體的阻力係數會疊合在一條曲線上。此曲線可推求不同直徑、不同流速下光滑圓球之阻力,亦即,可將實驗的結果普遍化。
<< 本章結束 >>








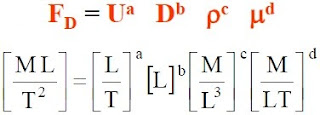













沒有留言:
張貼留言