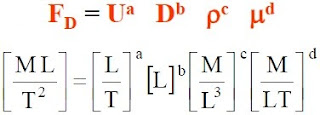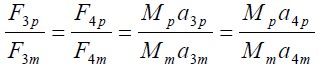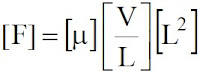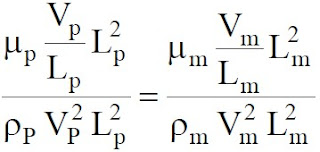(1) 雷諾數(Reynolds no.):
式中V為流速,μ為流體動力黏滯係數,ν為運動黏滯係數,L為特性長度。譬如管流中,L為管徑;尾流中,L 為物體直徑;邊界層流中,L為下游距離。
雷諾數皆代表慣性力和黏滯力之比,雷諾數小時,黏滯力大於慣性力,流場中的擾動會因黏滯力而衰減,流體流動穩定,流況為層流;雷諾數較大時,流場較不穩定,擾動容易增強,形成紊流。
(2) 福祿數(Froude no.):
式中V為流速,L為特性長度,g 為重力加速度,福祿數代表慣性力和重力之比。明渠流、波浪、船體模型試驗等問題中常用到福祿數。在明渠流中,特性長度為水深 h。
(3) 馬赫數(Mach number):
式中U為流速,C為音速。馬赫數代表慣性力與壓縮力之比。音速為壓力波(聲波)在流體中傳遞的速度。溫度為20oC下,水中的音速約為1480 m/s。在空氣中音速為340 m/s。當馬赫數Ma < 0.3時(水流流速< 440m/s,氣流流速U < 100 m/s)便滿足不可壓縮流場(Incompressible flow)的條件。
(4) 尤拉數(Euler number):
(5) 韋伯數(Weber number):
式中ρ 為流體密度,L為長度,V為流速,σ為流體的表面張力係數。韋伯數是紀念德國科學家韋伯(Weber)。
韋伯數代表慣性力和表面張力之比,若韋伯數小,則表示表面張力十分重要,譬如毛細管現象、小水滴、風吹過水面所引起的漣漪(表面張力波)等小尺度的問題。
一般大尺度的問題,韋伯數遠大於1.0,表面張力的作用便可以忽略。
★★★
若要達到"動力完全相似",必須模型與原型之所有無因次參數要相等,即
(Re)p = (Re)m , (Fr)p = (Fr)m , (Eu)p = (Eu)m , (W)p = (W)m ,(M)p = (M)m …
但模型試驗要符合每一種相似律在實際上十分困難,且幾乎不可能!所以通常只考慮流場中最重要之特性,而要求其相似。
→故最重要者為:
黏滯力 → Reynolds 相似律,(Re)p = (Re)m
重力 → Froude 相似律,(Fr)p = (Fr)m
ƒ壓力 → Euler 相似律,(Eu)p = (Eu)m
表面張力 → Weber 相似律,(W)p = (W)m
◎一般而言
管流(黏滯力主控) → 遵守 Reynolds 相似律
明渠流(重力主控) → 遵守 Froude 相似律
<< 本篇結束 >>