1.前言:
解決實際流體力學問題,通常有兩種途徑:
A.建立描述流動過程的微分方程式,給定初始條件、邊界條件,對微分方程求解(例如解 Navier-Stokes equations)
B.通過實驗,尋求流體運動過程的規律性
然而,實際流體的流動現象非常複雜,一般難以用微分方程來描述,即使能夠建立微分方程,也僅能以解析法(Analytical method)求得近似解(Approximate solution)。
因此,工程問題中經常需要進行模型(Model)試驗,以作為設計實體(Prototype)之參考。
譬如水壩、船隻、高樓結構物、飛機或汽車等,皆可在實驗室中以模型在水槽(Water flume)或風洞(Wind tunnel)中模擬其流況,以暸解實體所可能遇到的問題。
實驗室內之實驗控制性佳,可重複性高,是現場量測所難以企及的,故實驗室內的模型實驗是研究複雜流況所不可或缺的方法之一。
◎ 實驗(Experiments)分成兩種:
A. 物理模型試驗(Physical modeling):又稱水工模型試驗
B. 數值模式試驗(Numerical modeling):又稱數值模擬(Numerical simulation)
◎ 進行物理或數值實驗常遭遇之困難:
A. 變數(變因)太多,不易控制
B. 真實流況之尺度常太大或太小,無法以真實尺寸進行實驗
C. 數值模擬需要靠水工模型試驗數據或實地量測數據進行模式之參數檢定(Calibration)與結果驗証(Verification)。
◎ 進行水工模型試驗之前要先分析:
A. 物理模型須遵守哪種相似律(Law of Similitude)
B. 哪些是重要之變數,由因次分析(Dimensional analysis)得之
◎常用之物理量因次(常採MLT或FLT)
2. 流場相似性 (Similarity)
針對某一個工程問題進行模型實驗,實際流場與模擬流場之間必須滿足流場相似性的要求,模擬結果才能正確地應用於實體的設計。
模型相似有下列三種:
2-1. 幾何相似性 (Geometric Similarity):
指模型(Model)與原型(Prototype)間之幾何尺寸成比例。
2-2. 運動相似性似 (Kinematic similarity):
模擬流場與實際流場間相對應點之速度與加速度成比例,亦即模擬流場中任意兩點的流速比和實際流場中對應位置的流速比相同。
2-3. 動力相似性 (Dynamic Similarity):
指模型與原型間相對應點所受之各種外力成比例。外力可為分力或合力(各種分力包括:gravity,viscous,pressure....)
★完整之模型相似,須同時符合三者:(1)幾何 (2)運動 (3)動力 相似
⊙ 流場中常考慮之力:
(1) 慣性力(Inertia),FI
(2) 壓力(Pressure),Fp
(3) 重力(Gravity),FG
(4) 黏滯力(Viscosity),FV
(5) 表面張力(Surface Tension),FT
(6) 彈性力(Elasticity),FE
3.雷諾數(Reynolds no.)與福祿數(Froude no.)之推導:
依據:模擬流場與實際流場中流體所受之力必須成一定之比例(動力相似性),亦即模型之阻力係數必須與實體相同。
阻力係數(Drag coeff.)的定義為:
FD為物體所受之阻力,ρ為流體的密度,V為流速,A為物體迎風面的投影面積,阻力係數為無因次參數。
3-1. 黏滯阻力相似:
流體在流動的過程會受到的黏滯阻力與流體的黏滯係數μ及流體與物體接觸之表面積A有關
動力相似性要求阻力係數相等
整理可得
雷諾數(Reynolds no.):
若模型與實體的雷諾數相同,則代表黏滯阻力的阻力係數亦會相同,換言之,滿足阻力相似的要求。
3-2. 重力相似:
若流體所受到的重力必須遵守動力相似,而重力等於
重力所產生之阻力係數可表示為
整理可得
福祿數(Froude no.):
若模型與實體的福祿數相同,則模型與實體所受到的重力遵守重力相似,亦即滿足重力相似的要求。
<< 本章結束 >>





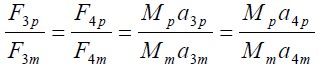








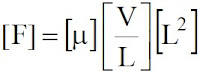

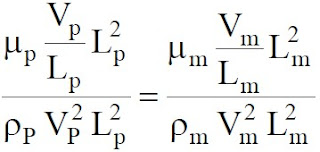








沒有留言:
張貼留言