靜水性能 (Hydrostatics)
進入本章前之先修科目:船舶穩度 (Stability)
【回顧一】阿基米德原理 (Archimedes’ Principle)
- 浮力(Buoyancy)等於排開同體積之液體重量,又稱為排水量(Displacement)△
- 船舶浮在水面上,其排開之液體體積稱為排水體積▽;且因船舶在鉛直方向處於平衡狀態,故浮力等於船舶重量W
 [註:γ為液體之重量密度]
[註:γ為液體之重量密度]
【回顧二】重心及浮心
- 船舶成千上萬之零件均有各自之重量,為了方便可將此眾多重量合成為經重心G垂直向下作用之單一力W
- 浮力△為作用在船舶浸水部分之體積所承受水壓之總合力,可以將其視為垂直向上集中作用於通過浸水體積形心(即浮心)B
- 由於船舶處於平衡狀態,因此W= △且在同一鉛直作用線
<< 船舶重量變化之重心計算 >>
【重心G在垂直方向之變化】
增加或移除重量將造成重心G位置之改變
- KG之改變
- TCG之改變
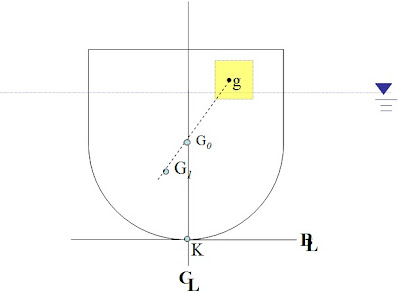
a. 增加重量w時:
重心將沿著原船舶重心G0及增加重量之重心g兩者的連線向增加重量方向轉移至G1
b. 移除重量w時:
重心將沿著原船舶重心G0及移除重量之重心g兩者的連線向遠離移除重量方向轉移至G1
重心首先遠離移動重量至G1(如同移除重量)…然後向重量新位置移動而為G2
首先,考慮重量直接增加在中線上
將會使新重心向增加重量方向移動 ...造成垂向重心高度 KG之改變
重心高度正確之改變距離為對龍骨K之力矩必須滿足:
==>
移除重量以相同方式處理,但力矩為減去
當移動重量時如同移除一重量w1,再增加另一重量w2
==>
==>
在此,可以將重心在垂直方向之變化寫成如下通式:
《 範例 》
步驟一:繪圖
步驟二:寫出通式
步驟三:將數值代入通式
<< 定傾中心 (Metacenter) 及 橫傾角 (List) 角度計算 >>
橫向定傾中心(MT):船舶在小角度Φ(< 10度)橫傾時之重要參考點
- 對小角度之橫傾,船舶如同繞著(MT)轉動
- KMT之值視船型而變,一般約10ft至30ft
同理,對縱向定傾中心 ML 也相同 (KML約1000ft)
因此,當船舶之裝載改變時其橫傾角度可以計算出來
《 範例 》
步驟一:由靜水曲線查出排水量為3960LT
步驟二:算出新重心高度(KG1)
步驟三:求出橫向重心位置(TCG1)
步驟四:定義G0G1及G0MT
<< 傾斜試驗 (Inclining Experiment) >>
目的:準確求出船舶在輕船時(Light Ship)的重心高度KG
- 首先量測輕船在正浮時之吃水,並由靜水曲線查出排水量△及KMT
- 橫向移動重量使船傾斜,紀錄傾斜時之角度正切值
注意事項:
- 船體傾斜角度,大船在1~1.5度、小船在1.5~3度;傾斜重量約佔全船排水量之0.5~1.0%
- 船體應使其自由浮起,纜繩應放鬆
- 應在風平浪靜之水域或塢內進行
- 各油水艙應灌滿或打空,以免自由液面影響試驗之準確結果
【重心縱向位置之改變】
考慮船舶為縱平浮、沒有橫傾
當重量 w 被加上時,吃水將產生變化
船舶將以以浮面中心F轉動
- 很明顯地前方吃水將會改變
- 同樣地後方吃水也將改變
前後吃水差即為俯仰差之變化:
以圖形表示如下:首先以一直線表示船舶之初始狀態
當重量加上後,船舶將繞F點轉動
欲求出吃水變化必須考慮兩情況:
1. 由於增加重量w所造成的平行下沉(parallel sinkage)
(a) TPI可由靜水曲線查出
(b) 假設重量加在浮面中心F處
(c) 增加之重量w,造成整體平行下沉一小段距離
2. 由於重量w與浮面中心F間之距離d所產生的俯仰力矩對吃水造成的俯仰差變化
(a) MT1"可由靜水曲線查出
(b) 重量w與浮面中心F相距d產生的力矩,造成船舶繞F轉動
(c) 此轉動造成船舶一端下沉,另一端上升
(d) 上升或下沉之程度將視浮面中心F之位置而定
因此,將因平行下沉及俯仰力矩成之吃水變化加到原吃水上,最終之吃水即可獲得:
由於δTrim 為針對整體船長,因此,須求出此俯仰差變化在船艏及船艉各分配多少:
欲求俯仰差分布,考慮下面之相似三角形:
- 大三角形為總俯仰差變化 δTrim
- 綠色斜線三角形表示 δTfwd
- 黃色斜線三角形表示 δTaft
知道如何求平行下沉及俯仰差度吃水之變化後,套入下式,船舶艏艉之最終吃水即可求出:
《 範例 》
首先,先繪出如下之吃水示意圖:
步驟一: 求出平行下沉
步驟二: 求俯仰差變化
步驟三:相似三角形關係
步驟四:求出艏艉吃水之總變化
艏吃水:
艉吃水:
<< 本章結束 >>


























































沒有留言:
張貼留言