船舶穩度

《 船舶穩度 》
船舶之穩度為船舶本身所具有抵抗傾側，翻覆以及當外力消除後回復到原來正浮位置之能力表示。

【船舶穩度相關名詞定義】

• 完整穩度(Intact Stability)：船舶在完整無損時之穩度。
• 受損或浸水穩度(Damaged or Flooding Stability)：船舶在受損浸水狀態時的穩度。
• 靜穩度(Statical Stability)：在沒有角速度變化的情況下，船舶傾斜時扺抗傾側的能力。
• 動穩度(Dynamical Stability)：在伴隨有角速度變化的情況下，船舶傾斜時扺抗傾側的能力。
• 橫向穩度(Transverse Stability)：船舶本身所具有的抵抗橫向傾側，翻覆之能力。

《 原理 》
當處在靜態平衡之船舶受到外力作用時，其平衡狀態將改變：
風力及水線下相反方向之水阻力將造成對浮面中心之外力偶矩

而船舶對以浮面中心為樞點之外力偶矩的回應是使浮力中心Ｂ移動

1. 由於重量沒有改變且其分布也沒有改變，因此重心位置Ｇ不變
2. 由於浸水體積形狀改變，因此浮力中心Ｂ隨之移動
3. 由於重力作用線及浮力作用線將不再共線，因此由船體之傾斜將產生一內力偶矩

儘管船舶因風力而傾斜，但外力偶矩促使船舶產生內力偶矩來抗衡，以達平衡狀態

《 內力偶矩 》

1. 重力作用線及浮力作用線分開所造成
2. 重力及浮力兩者之作用線分開的距離為 GZ，稱之為力臂 ；力臂之大小為橫傾角Φ的函數

《 扶正力矩 (Righting Moment) 》

1. 力矩為力作用線對某一點有一段距離作用而產生的
2. 重力及浮力兩者之作用線距離為GZ，稱之為扶正力臂；此內力矩稱之為扶正力矩(Righting Moment)

《 完整靜穩度曲線 》
扶正力臂之長度會隨橫傾角Φ變化而有所不同

1. 完整靜穩度曲線繪於第一及第三象限(第三象限表示向左舷傾斜)；因為船左右對稱，一般只繪出向右舷傾斜之曲線。
2. 在原點處切線之斜率為初穩度之定傾高度GMT，當GMT大時稱為剛性船(stiff ship)，較小時稱為柔性船(tender ship)。

[A] 橫傾角Φ為0度時扶正力臂為0，浮力及重力作用線共線，沒有力矩產生

[B] 橫傾角增加至25度時, GZ 為 2.5ft.

[C] 在 GZ max 時扶正力矩為最大值；若外力矩大於此最大扶正力矩，則船將繼續傾斜直到翻覆

[D] 橫傾角繼續增加，而 GZ減小，亦即扶正力矩減小

[E] 橫傾角增加至 G 及 B 作用線又達到共線，此處 GZ 為零，已無扶正力矩，超過此點船將翻覆而不能扶正

《 船舶初穩度 (Initial Stability) 》

1. 當船舶的橫傾角度很小時(<10度)之穩度稱為初穩度
2. 初穩度以定傾高度GMT表示
3. GMT為完整靜穩度曲線在原點之切線斜率

[A] 船舶正浮，處於穩定平衡(stable equilibrium)

[B] 船舶處於中性平衡(neutral equilibrium)

[C] 船舶無法正浮，向左右兩邊傾斜至偃息角(angle of llol)，為不穩定平衡(unstable equilibrium)

《 穩度交叉曲線 (Cross Curves of Stability) 》

1. 穩度交叉曲線以排水量為橫座標，扶正力臂為縱座標，每一條曲線表示某一橫傾角之扶正力臂。
2. 由於船舶之重心高度KG會隨不同裝載情況而變化，且在設計階段也不能知道正確重量，因此大多數的穩度交叉曲線都假設KG=0。
3. 由於船舶的真正KG一定在龍骨上方，由交叉曲線所查出的扶正力臂其修正量均為減除。

《 扶正力臂之正弦(Sine)及餘弦(Cosine)之修正 》

【 正弦修正 (由於重心G之垂向改變) 】
在穩度交叉曲線中，扶正力臂之數據由下面之假設而獲得：

但，此並非真實，然而此方法可以使交叉曲線在所有吃水下得以通則化；欲求出正確的扶正力臂，必須利用正弦修正(Sine correction)將重心轉移到真正的KG位置

[A] 當船舶橫傾後，浮力中心 B 將會向傾斜一方轉移，此轉移產生扶正力臂

[B] 從穩度交叉曲線所找出的扶正力臂數值為假設G0 位於龍骨，但此G0Z0並非真正的扶正力臂

[C] 真正的重心位置Gv給定時，真正的KG值即可獲知

[D] 正弦修正

【 餘弦修正 (由於重心G之橫向改變) 】

【合併正弦及餘弦修正】

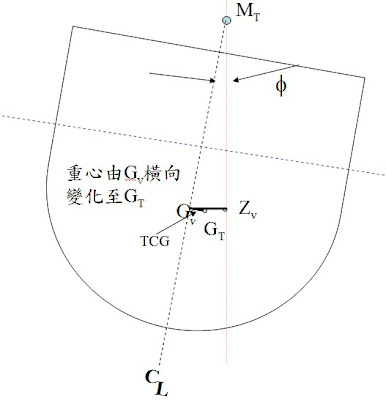
《 自由液面效應 (Free Surface Effect) 》

1. 對於沒有全滿的液艙，液面將可自由移動。當船體傾斜時艙內液體隨之移動，就如同重量之移動，將會造成重心位置改變。
2. 當船舶傾斜時，因液面之移動使重心由G水平移動至G1，而扶正力臂亦由GZ縮減至G1Z1。
3. 此現象夠如同重心由G提升至GV，因此自由液面修正量FSC (Free Surface Correction)即為重心虛升之高度GGV。
4. 對於小角度傾斜(<5~7度)而言：

<< 本章結束 >>